2010年
- 研究集会
-
11月25日 (木) 10時00分 〜 11月26日 (金) 16時30分 (京都大学理学部3号館 (数学教室) 110講演室) Non Commutative Geometry and Number Theory - RIMS Special Year on Non Commutative Geometry
- (火) 2010年01月05日
集中講義 14時00分 〜 15時30分 (京都大学理学部3号館 (数学教室) 127大会議室) Paul Sweeting 氏 (University of Kent) Enterprise Risk Management - 1. Introduction (概要)
- (水) 2010年01月06日
集中講義 10時30分 〜 12時00分 (京都大学理学部3号館 (数学教室) 127大会議室) Paul Sweeting 氏 (University of Kent) Enterprise Risk Management - 2. Financial Institutions (金融機関のリスク) 集中講義 14時00分 〜 15時30分 (京都大学理学部3号館 (数学教室) 127大会議室) Paul Sweeting 氏 (University of Kent) Enterprise Risk Management - 3. The Mathematics of ERM (ERMの数学的基礎)
- (木) 2010年01月07日
集中講義 10時30分 〜 12時00分 (京都大学理学部3号館 (数学教室) 127大会議室) Paul Sweeting 氏 (University of Kent) Enterprise Risk Management - 4. Some case studies (ERMの実例)
- (金) 2010年01月08日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) David Smyth (Harvard) Log minimal model program for moduli spaces of pointed curves 13時30分 〜 14時30分 数論合同セミナー (京都大学理学部3号館 (数学教室) 152号室) 森 伸吾 (京大・理) 有限体上の２元３次形式の空間の付随するGauss和について 14時45分 〜 15時45分 数論合同セミナー (京都大学理学部3号館 (数学教室) 152号室) 谷口 隆 (神戸大・理) 概均質ベクトル空間の「軌道型」L関数と関数等式 15時00分 〜 16時00分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 109号室) 津川 光太郎 (名古屋大学・多元数理) Local well-posedness for the Zakharov system in one space dimension 16時15分 〜 17時45分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 109号室) Justin Holmer (Browin University) Dynamics of solitons
- (火) 2010年01月12日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 藤原 耕二 (東北大・情報) Subgroups in the group of interval exchange transformations
- (金) 2010年01月15日
13時30分 〜 14時30分 数論合同セミナー (京都大学理学部3号館 (数学教室) 152号室) 金子 元 (京大・理) On the binary expansions of algebraic irrational numbers 14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 上原 崇人 (九州大学・大学院数理学府) 有理曲面上の自己同型写像について
- (火) 2010年01月19日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 梶野 直孝 (京大・情報) Spectral asymptotics for Laplacians on Sierpinski carpets
- (金) 2010年01月22日
14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 西澤 由輔 (首都大学東京・理工学研究科) ヘテロ次元接触を含むサイクルから導き出されるストレンジアトラクターについて
- (火) 2010年01月26日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 岡田 崇 (京大・数理研) Homological mirror symmetry of Fermat polynomials and some related topics
- (金) 2010年01月29日
14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 石井 豊 (九州大学大学院数理科学研究院) Homotopy shadowing theorem の証明について
- (金) 2010年02月05日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部3号館 (数学教室) 110講演室) Fanny Kassel (Universite Paris-Sud 11) Clifford-Klein forms of rank-one semisimple groups
- (月) 2010年02月08日
集中講義 13時00分 〜 14時30分 (京都大学理学部3号館 (数学教室) 108号室) 金子 邦彦 氏 (東京大学大学院総合文化研究科) 数学と自然科学・社会科学III --「生命とは何か」を理解するための数理 15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) Vladimir Sharko (National Academy of Sciences of Ukraine) The L^2- invariants and Morse Numbers of Manifolds
- (火) 2010年02月09日
集中講義 13時00分 〜 14時30分 (京都大学理学部3号館 (数学教室) 108号室) 金子 邦彦 氏 (東京大学大学院総合文化研究科) 数学と自然科学・社会科学III --「生命とは何か」を理解するための数理
- (水) 2010年02月10日
集中講義 13時00分 〜 14時30分 (京都大学理学部3号館 (数学教室) 108号室) 金子 邦彦 氏 (東京大学大学院総合文化研究科) 数学と自然科学・社会科学III --「生命とは何か」を理解するための数理
- (金) 2010年02月12日
15時30分 〜 17時00分 関西確率論セミナー (京都大学理学部3号館 (数学教室) 552号室) Freddy Delbaen (ETH, Zurich) Mod-gaussian convergence results with applications.
- (火) 2010年02月16日
10時30分 〜 12時30分 Special seminar on representation theory (京都大学理学部3号館 (数学教室) 108号室) Dan Ciubotaru (Utah) On formal degrees for discrete series of classical affine Hecke algebras. 15時00分 〜 18時00分 微分トポロジーセミナー (京都大学理学部6号館609号室) 中島 啓 (京大・数理研) Donaldson = Seiberg-Witten from Mochizuki's formula and instanton counting
- (水) 2010年02月17日
13時30分 〜 15時00分 臨時セミナー (京都大学理学部3号館 (数学教室) 552号室) 濱名 裕治 (熊本大学大学院自然科学研究科) Wiener sausage の体積の期待値の漸近展開について
- (月) 2010年02月22日
15時30分 〜 16時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 108号室) Serge Alinhac (Universite de Paris-Sud, Orsay) Stability and blowup at infinity for quasilinear wave equations, I 16時45分 〜 17時45分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 108号室) Wilhelm Schlag (University of Chicago) On decay of linear waves on curved backgrounds
- (火) 2010年02月23日
15時00分 〜 16時00分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 108号室) Serge Alinhac (Universite de Paris-Sud) Stability and blowup at infinity for quasilinear wave equations, II 16時15分 〜 17時15分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 108号室) Wilhelm Schlag (University of Chicago) On concentration compactness for critical wave maps
- (水) 2010年02月24日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部3号館 (数学教室) 305号室) Jason Manning (SUNY) Virtually geometric words and Whitehead's algorithm
- (木) 2010年02月25日
15時00分 〜 16時00分 第21回 GCOE tea time (京都大学理学部3号館 (数学教室) 306号室) 佐藤 文敏氏 (香川高専) Tautological ring of moduli of curves via localization
- (月) 2010年03月08日
集中講義 15時00分 〜 17時00分 (京都大学理学部3号館 (数学教室) 110講演室) Robert Penner 氏 (Aarhus Univ./Univ. of Southern California) GCOE集中講義 (1) "Proteins and their intrinsic geometry.html"
- (火) 2010年03月09日
集中講義 15時00分 〜 17時00分 (京都大学理学部3号館 (数学教室) 110講演室) Robert Penner 氏 (Aarhus Univ./Univ. of Southern California) GCOE集中講義 (2) "Discrete models of protein geometry.html"
- (水) 2010年03月10日
集中講義 15時00分 〜 17時00分 (京都大学理学部3号館 (数学教室) 110講演室) Robert Penner 氏 (Aarhus Univ./Univ. of Southern California ) GCOE集中講義 (3) "Protein moduli space.html"
- (金) 2010年03月12日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Thorsten Weist (Wuppertal) Localization in quiver moduli spaces 13時00分 〜 14時30分 離散幾何解析セミナー (京都大学理学部3号館 (数学教室) 552号室) Ravi Montenegro氏 (University of Massachusetts Lowell) Mixing times and new Cheeger inequalities for finite Markov chains 13時00分 〜 14時30分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Jacopo Stoppa (Cambridge) Some higher-rank sheaves on Calabi-Yau threefolds and Gromov-Witten invariants
- (水) 2010年03月17日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部3号館 (数学教室) 305号室) Jacopo Stoppa (University of Cambridge) On the algebro-geometric stability of extremal metrics
- (金) 2010年03月19日
15時30分 〜 17時00分 関西確率論セミナー (京都大学理学部3号館 (数学教室) 552号室) 福島 竜輝 ( 東工大) Brownian motion in heavy tailed Poissonian potentials
- (水) 2010年03月24日
- (金) 2010年04月09日
13時00分 〜 14時30分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Alexander Usnich (Miami) Non-commutative cluster mutations 14時00分 〜 17時00分 京都力学系セミナー (京都大学理学部6号館609号室) 宇敷 重廣 (京都大学大学院・人間・環境学研究科) ２パラメータの複素力学系について
- (火) 2010年04月13日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 本多 正平 (京大・数理研) リッチ曲率が非負である多様体上の調和関数と多様体の収束
- (金) 2010年04月16日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 山田 紀美子 (京都大学) Birational aspects of moduli scheme of sheaves on a surface 14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 柴山 允瑠 (京都大学・数理解析研究所) 変分法による超8の字解の存在証明 14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 柴山 允瑠 (京大・数理研) 変分法による超8の字解の存在証明
- (火) 2010年04月20日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 吉田 尚彦 (明治大・理工) Torus fibrations and localization of index
- (金) 2010年04月23日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Yoshinori Gongyo (Univ. of Tokyo) On weak Fano varieties with log canonical singularities 13時00分 〜 14時30分 離散幾何解析セミナー (京都大学理学部3号館 (数学教室) 552号室) Robert Sinclair 氏 (沖縄科学技術研究基盤整備機構/Okinawa Institute of Science and Technology) What causes Flat Dendritic Bifurcations? 15時30分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 伊藤 敏和・山岸 義和 (龍谷大学 理工学部) Transversality of linear distributions with spheres in the complex space
- (火) 2010年04月27日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 深谷 友宏 (京大・理) Sublinear Higson corornae of Euclidean cones
- (金) 2010年05月07日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 稲場 道明 (京大・理) Smoothness of the moduli space of complexes of coherent sheaves on an abelian or a projective K3 surface
- (火) 2010年05月11日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 山下 真 (東大・数理) TBA 15時00分 〜 16時00分 第23回 GCOE tea time (京都大学数理解析研究所402号室) 桑原 敏郎 (数理解析研究所) 有理Cherednik代数の超局所化と表現論
- (金) 2010年05月14日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 入谷 寛 (京大・理) TBA 14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) Pawel Pilarczyk (University of Minho) Finite resolution dynamics
- (火) 2010年05月18日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 柴山 允瑠 (京大・数理研) 4体問題の超8の字解の変分法による存在証明
- (水) 2010年05月19日
16時30分 〜 17時30分 談話会 (京都大学数理解析研究所110号室) Yongnam Lee (京大・数理研) Algebraic surfaces of general type with vanishing geometric genus
- (金) 2010年05月21日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 松下 大介 (北海道大学) 単位円上の Abelian fibration の相対極小モデルについて 14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 亀山 敦 (岐阜大学) カントール的ジュリア集合のコーディングについて 15時00分 〜 16時00分 数論合同セミナー (京都大学理学部3号館 (数学教室) 152号室) 津嶋 貴弘 (東大・数理) On the stable reduction of 
15時30分 〜 17時00分 関西確率論セミナー (京都大学理学部3号館 (数学教室) 552号室) 矢野 孝次 (東工大) 道路着色に従う有向グラフ上のランダムウォーク
- (火) 2010年05月25日
13時30分 〜 14時30分 第24回 GCOE tea time (京都大学数理解析研究所402号室) 本多 正平 (数理解析研究所) Riemann多様体の収束・崩壊とRicci曲率 15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 佐野 友二 (九州大・数理) ファノ多様体のK安定性についての考察
- (水) 2010年05月26日
14時40分 〜 15時40分 大談話会 (京都大学数理解析研究所420大会議室) Ken-Ichi Yoshikawa (京大・理) Analytic torsion and automorphic forms 16時30分 〜 17時30分 大談話会 (京都大学数理解析研究所420大会議室) 葉廣 和夫 (京大・数理研) Category of bottom tangles and quantum invariants
- (金) 2010年05月28日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 小木曽 啓示 (大阪大学) Bounded derived categories of very simple manifolds
- (火) 2010年06月01日
15時00分 〜 16時00分 微分トポロジーセミナー (京都大学理学部6号館609号室) Chikako Mese (Johns Hopkins University) Harmonic maps between singular spaces 16時00分 〜 17時00分 微分トポロジーセミナー (京都大学理学部6号館609号室) George Daskalopoulos (Brown University) Superrigidity of hyperbolic buildings 16時00分 〜 17時30分 NLPDEセミナー (3号館251号室) Matthias Hieber (TU Darmstadt) Stability properties of Ekman boundary layers
- (水) 2010年06月02日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) 阿部 拓郎 (京大・理) コクセター型超平面配置の補空間と不変式論
- (金) 2010年06月04日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Yongnam Lee (Sogang University) Sogang UniversityLog canonical models of moduli space of stable curves of genus 4 13時00分 〜 14時30分 離散幾何解析セミナー (京都大学理学部3号館 (数学教室) 552号室) 田中 利幸氏 (京都大学大学院情報学研究科) 圧縮センシング：数理と応用
- (火) 2010年06月08日
15時00分 〜 16時00分 第25回 GCOE tea time (京都大学数理解析研究所402号室) 中村 伊南沙 (数理解析研究所) 曲面結び目と曲面ブレイド、特に自明なトーラスの被覆の形をした曲面結び目について
- (水) 2010年06月09日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 110講演室) Boris Tsygan (Northwestern University) Microlocal methods in symplectic geometry
- (金) 2010年06月11日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 安武 和範 (九州大学) On weak Fano manifolds with projective space bundle structure 10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 安武 和範 (九州大学) On weak Fano manifolds with projective space bundle structure 13時00分 〜 14時30分 微分トポロジーセミナー (京都大学理学部６号館８０９号室) Boris Tsygan (Northwestern University) Oscillatory modules 14時00分 〜 17時00分 京都力学系セミナー (京都大学理学部6号館609号室) 上田 哲生 (京大・理) Critically finite holomorphic maps on projective spaces 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部３号館251号室) 本多 正平 (京大・数理研) リーマン多様体上の調和関数について
- (水) 2010年06月16日
16時30分 〜 17時30分 談話会 (京都大学数理解析研究所110号室) Kenshi Miyabe (京大・数理研ポスドク) Algorithmic randomness
- (金) 2010年06月18日
15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部３号館251号室) 出来 光夫 (北海道大・理) 変動指数関数空間における作用素の有界性 15時30分 〜 17時00分 関西確率論セミナー (京都大学理学部3号館 (数学教室) 552号室) 梶野 直孝 (京大・情報学) Sierpinski gasket上の測度論的Riemann構造に対する熱核の漸近挙動解析
- (火) 2010年06月22日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 塚本 真輝 (京大・理) インスタントンを持たない開４次元多様体 15時00分 〜 16時00分 第26回 GCOE tea time (京都大学数理解析研究所402号室) 和田 堅太郎 (数理解析研究所) Blocks of category O for rational Cherednik algebras and of cyclotomic Hecke algebras of type G(r,p,n)
- (水) 2010年06月23日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 110講演室) Teruyoshi Yoshida (University of Cambridge) Geometric realization of local Langlands correspondence
- (金) 2010年06月25日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 岩成 勇 (京都大学・数理研) Tannakian aspects of higher derived categories 14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 吉村 浩明 (早稲田大学・理工学術院) 力学系のネットワーク構造の理解へ向けて ー ディラック幾何，内部接続系および変分構造について ー 14時00分 〜 15時00分 整数論講演 (京都大学理学部3号館 (数学教室) 127大会議室) 三枝 洋一 (九大・数理) Cuspidal representations in the l-adic cohomology of the Rapoport-Zink space for GSp(4) 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部３号館251号室) 水野 将司 (東北大学) porous medium方程式の解に対するH\.html"older評価とその応用
- (水) 2010年06月30日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) Kazuya Kato (University of Chicago) Iwasawa theory for modular forms and incarnation of Zeta
- (金) 2010年07月02日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Hisanori Ohashi (京大・数理研) Hutchinson-Weber involutions degenerate exactly when the Jacobian is Comessatti. 15時00分 〜 16時30分 GCOE特別講義 (京都大学数理解析研究所110号室) Bahman Kalantari (Department Of Computer Science, Rutgers University) Polynomial Root-Finding Methods Whose Basins of Attraction Approximate Voronoi Diagram 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部６号館２５１号室) Nahas, Joules (University of California) On the persistent properties of solutions to semi-linear Schrodinger equations
- (水) 2010年07月07日
16時30分 〜 17時30分 談話会 (京都大学数理解析研究所110号室) 上田 肇一 (京大・数理研) 反応拡散系にみられるパターンダイナミクス：生物の環境適応性への応用
- (金) 2010年07月09日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 星 裕一郎 (京大・数理研) 双曲的曲線の非幾何学的な副 p Galois 切断の存在 14時00分 〜 18時00分 京都力学系セミナー (京都大学理学部6号館609号室) 深谷 友宏 (京大・理) Asymptotic distribution of critical values 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部３号館２５１号室) 和 田出秀光 (国立台湾大学) The existence of positive solutions to the semilinear elliptic equation involving the Sobolev-Hardy critical terms
- (火) 2010年07月13日
15時00分 〜 16時00分 第27回 GCOE tea time (京都大学数理解析研究所402号室) 嶽村 智子 (京都大学数学教室) 斜積拡散過程とその時間変更 15時30分 〜 17時00分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 305号室) Benjamin Dodson (University of California) Global well-posedness and scattering for the defocusing, $L2$-critical, nonlinear Schrodinger equation when $d \geq 3$.
- (水) 2010年07月14日
15時30分 〜 17時00分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 305号室) Benjamin Dodson (University of California) Global well-posedness and scattering for the defocusing, $L2$-critical, nonlinear Schrodinger equation when $d \geq 3$. 16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) 矢野 裕子 (京大・理) 安定レヴィ過程に対する処罰問題について
- (月) 2010年07月19日
研究集会 10時00分 〜 17時40分 (京都大学理学部3号館 (数学教室) 108号室) ミニ研究集会「数論幾何とその周辺」
- (火) 2010年07月20日
13時30分 〜 14時30分 第28回 GCOE tea time (京都大学数理解析研究所402号室) 森山 貴之 (数理解析研究所) 葉層構造と横断的幾何構造とそのモジュライ 15時00分 〜 17時00分 調和解析セミナー (京都大学理学部6号館604号室) Jae-Hyun Yang (Inha University) Polarized Real Tori
- (金) 2010年07月23日
10時00分 〜 11時30分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 藤原 宏志 (京都大学情報学研究科) 多倍長計算・高精度計算による数値計算の拡がり - 計算機での数値処理と基本的なアルゴリズム 10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Edward Segal (Imperial College London) Equivalences between Landau-Ginzburg B-models 13時00分 〜 14時30分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 山本 野人 (電気通信大学情報工学科) 常微分方程式の精度保証付き計算の理論と技法 - 精度保証付き数値計算の概要 14時45分 〜 16時15分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 藤原 宏志 (京都大学情報学研究科) 多倍長計算・高精度計算による数値計算の拡がり - 計算誤差と数値計算の信頼性 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 305号室) 新 國 裕昭 (東京大学) On the degenerate spectral gaps of the one-dimensional Schr\"odinger operators with the periodic $\delta^{(1)}$-interactions 16時30分 〜 18時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 山本 野人 (電気通信大学情報工学科) 常微分方程式の精度保証付き計算の理論と技法 - 精度保証の基本的な技法
- (土) 2010年07月24日
10時30分 〜 12時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 藤原 宏志 (京都大学情報学研究科) 多倍長計算・高精度計算による数値計算の拡がり - 高精度離散化と多倍長計算による高精度数値計算 13時15分 〜 14時45分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 山本 野人 (電気通信大学情報工学科) 常微分方程式の精度保証付き計算の理論と技法 - 常微分方程式初期値問題の精度保証と数値計算例 15時00分 〜 16時30分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 藤原 宏志 (京都大学情報学研究科) 多倍長計算・高精度計算による数値計算の拡がり - 物理学・工学における高精度数値計算の利用例
- (水) 2010年07月28日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) Dai Tamaki (信州大学理学部) Combinatorial configuration spaces
- (金) 2010年09月03日
15時30分 〜 17時00分 NLPDEセミナー (京都大学理学部３号館251号室) Tadahiro Oh (Princeton University) Normal forms and the "upside-down" I method: growth of higher Sobolev norms for periodic NLS.
- (月) 2010年09月06日
16時00分 〜 17時00分 代数トポロジー特別講演 (京都大学理学部6号館609号室) S. Theriault (University of Aberdeen) Power maps on p-regular Lie groups
- (火) 2010年09月07日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) Andrzej Zuk (Universite Paris 7) On a problem of Atiyah
- (月) 2010年10月04日
10時30分 〜 12時00分 整数論連続講義 (京都大学理学部3号館 (数学教室) 108号室) 肥田 晴三 (UCLA) Arithmetic invariant and Geometry
- (水) 2010年10月06日
13時00分 〜 14時30分 幾何学特別講義 (京都大学理学部3号館 (数学教室) 110講演室) Daniel Ruberman (Brandeis University) Seiberg-Witten invariants and index theory on periodic-end manifolds 16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) Hiroshi Iritani (kyoto university) Quantization and modularity in Gromov-Witten theroy
- (木) 2010年10月07日
15時30分 〜 17時00分 幾何学特別講義 (京都大学理学部3号館 (数学教室) 110講演室) Daniel Ruberman (Brandeis University) Seiberg-Witten invariants and index theory on periodic-end manifolds
- (金) 2010年10月08日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 森脇 淳 (京都大学) Toward Dirichlet's unit theorem on arithmetic varieties 14時00分 〜 17時00分 京都力学系セミナー (京都大学理学部6号館609号室) David Blazquez-Sanz (Universidad Sergio Arboleda) Differential Galois approach to some Sturm-Liouville problems and applications to dynamical systems 15時00分 〜 17時00分 整数論連続講義 (京都大学理学部3号館 (数学教室) 108号室) 肥田 晴三 (UCLA) Arithmetic invariant and Geometry 15時30分 〜 17時00分 関西確率論セミナー (京都大学理学部3号館 (数学教室) 552号室) Yangzi Hu (Huazhong University of Science and Technology) Stochastic Lotka-Volterra model with multiple delays 15時30分 〜 17時00分 幾何学特別講義 (京都大学理学部3号館 (数学教室) 110講演室) Daniel Ruberman (Brandeis University) Seiberg-Witten invariants and index theory on periodic-end manifolds 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 251号室) 中西 賢次 (京大・理) 非線形 Klein-Gordon 方程式の基底エネルギーを超えた大域動力学 16時30分 〜 18時00分 表現論セミナー (京都大学理学部3号館 (数学教室) 109号室) 荒川 知幸 (奈良女子大・理) W-algebras and their representations
- (火) 2010年10月12日
13時00分 〜 14時30分 幾何学特別講義 (京都大学理学部3号館 (数学教室) 110講演室) Daniel Ruberman (Brandeis University) Seiberg-Witten invariants and index theory on periodic-end manifolds 13時30分 〜 14時30分 整数論特別講演会 (京都大学理学部3号館 (数学教室) 108号室) Matteo Longo (Padova大学) Quaternion algebras, Heegner points and arithmetic of Hida families (joint work with S.Vigni) 14時45分 〜 15時45分 整数論特別講演会 (京都大学理学部3号館 (数学教室) 108号室) Francois Brunault (ENS) L-functions of elliptic curves over number fields: conjectures and examples 15時00分 〜 16時00分 第29回 GCOE tea time (京都大学数理解析研究所402号室) 近藤 剛史 (神戸大学) 距離関数の凸性と群作用の固定点 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 552号室) 三浦 英之 (大阪大学・理) 非圧縮Navier-Stokes流に対するLiouville型定理とその応用 16時00分 〜 17時00分 整数論特別講演会 (京都大学理学部3号館 (数学教室) 108号室) Jayce Getz (McGill大学) Relative endoscopy and arithmetic geometry of Shimura varieties
- (水) 2010年10月13日
13時00分 〜 14時30分 幾何学特別講義 (京都大学理学部3号館 (数学教室) 110講演室) Daniel Ruberman (Brandeis University) Seiberg-Witten invariants and index theory on periodic-end manifolds
- (金) 2010年10月15日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 山木 壱彦 (京大) Geometric Bogomolov conjecture for abelian varieties and some results for those with some degeneration. 13時00分 〜 15時00分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 251号室) Tadahiro Oh (Princeton University) Hamiltonian Systems and Invariant Measures 14時00分 〜 17時00分 京都力学系セミナー (京都大学理学部6号館609号室) 木坂 正史 (京大・人間・環境学研究科) Smoothness of hairs for some entire functions (joint work with Mitsuhiro Shishikura) 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 251号室 ) 竹田 寛志（東北大学・理） (東北大学大学院理) 非線形消散型梁方程式の解の大域挙動について
- (水) 2010年10月20日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) Yukinobu Toda (The University of Tokyo・IPMU) Curve counting theories via stable objects
- (金) 2010年10月22日
13時00分 〜 14時30分 離散幾何解析セミナー (京都大学理学部3号館 (数学教室) 552号室) 平井 広志氏 (京都大学数理解析研究所) 多品種流について 13時00分 〜 15時00分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 251号室 ) Tadahiro Oh (Princeton University) Hamiltonian Systems and Invariant Measures 2 15時00分 〜 16時30分 臨時微分トポロジーセミナー (京都大学理学部3号館 (数学教室) 109号室) 石渡 聡 (筑波大学) Heat kernel estimates on non-compact gluings 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 251号室) 渡辺 達 (京産大) Asymptotic behavior of ground states of quasilinear Schrodinger equations
- (月) 2010年10月25日
集中講義 15時00分 〜 17時00分 (京都大学理学部3号館 (数学教室) 108号室) Mei Kobayashi 氏 (IBM Research-Tokyo) 数学と自然科学・社会科学 III "From Information Retrieval to Web Mining: a mathematical tour.html"
- (火) 2010年10月26日
13時30分 〜 14時30分 第30回 GCOE tea time (京都大学数理解析研究所402号室) 深谷 友宏 (京都大学数学教室) Coarse geometry and Topology of Higson corona 集中講義 15時00分 〜 17時00分 (京都大学理学部3号館 (数学教室) 108号室) Mei Kobayashi 氏 (IBM Research-Tokyo) 数学と自然科学・社会科学 III "From Information Retrieval to Web Mining: a mathematical tour.html" 15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 桑田 和正 (お茶の水女子大・理) Couplings of Brownian motions associated with a time-dependent metric
- (水) 2010年10月27日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) 水町 徹 (九州大学・数理) KP-II方程式のline-soliton解の安定性
- (金) 2010年10月29日
13時30分 〜 15時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 杉田 洋氏 (大阪大学理学研究科) モンテカルロ法，乱数，および疑似乱数 -- モンテカルロ法の数学的定式化 15時30分 〜 17時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 杉田 洋氏 (大阪大学理学研究科) モンテカルロ法，乱数，および疑似乱数 -- 乱数
- (土) 2010年10月30日
13時30分 〜 15時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 杉田 洋氏 (大阪大学理学研究科) モンテカルロ法，乱数，および疑似乱数 -- 疑似乱数 15時30分 〜 17時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 杉田 洋氏 (大阪大学理学研究科) モンテカルロ法，乱数，および疑似乱数 -- モンテカルロ積分
- (火) 2010年11月02日
集中講義 18時15分 〜 19時30分 (京都大学理学部3号館 (数学教室) 110講演室) 伊藤 哲史 (京都大学理学研究科数学教室 ) 数学吉田塾・連続講義「楕円曲線の有理点」
- (金) 2010年11月05日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室 ) 川谷 康太郎 (大阪大学) Stability conditions and the autoequivalence subgroup of K3 surfaces 13時00分 〜 14時30分 数論合同セミナー (京都大学理学部3号館 (数学教室) 152号室) Francis Brown ( Jussieu) On the coalgebra structure of motivic multiple zeta values 14時00分 〜 17時00分 京都力学系セミナー (京都大学理学部6号館609号室) Boris Zhilinski (Universite du Littoral Cote d'Opale) Hamiltonian monodromy. Quantum physics applications.
- (火) 2010年11月09日
集中講義 18時15分 〜 19時30分 (京都大学理学部3号館 (数学教室) 110講演室) 伊藤 哲史 (京都大学理学研究科数学教室 ) 数学吉田塾・連続講義「楕円曲線の有理点」
- (水) 2010年11月10日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) 平岡 裕章 (広島大学) 有理写像と最尤推定復号：力学系からの符号理論へのアプローチ
- (金) 2010年11月12日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 吉川 謙一 (京大・理) Singularities and analytic torsion 14時30分 〜 16時30分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 縫田 光司氏 (産業技術総合研究所 情報セキュリティ研究センター) 数学と情報セキュリティ科学を巡る知の循環、その実例として--フィンガープリント符号とガウスの求積法 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 251号室) Tomoyuki Miyaji (Kyoto University・RIMS) Bifurcation analysis to the Lugiato-Lefever equation in one space dimension
- (土) 2010年11月13日
10時00分 〜 12時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 縫田 光司氏 (産業技術総合研究所 情報セキュリティ研究センター) 数学と情報セキュリティ科学を巡る知の循環、その実例として--擬似乱数の安全性評価とルート２の二進数展開 14時00分 〜 16時00分 「計算機を用いた数学研究」GCOEセミナー (京都大学理学部3号館 (数学教室) 110講演室) 縫田 光司氏 (産業技術総合研究所 情報セキュリティ研究センター) 数学と情報セキュリティ科学を巡る知の循環、その実例として--量子情報セキュリティの長期的安全性と凸集合の幾何学
- (月) 2010年11月15日
集中講義 13時00分 〜 14時30分 (京都大学理学部3号館 (数学教室) 110講演室) 甘利 俊一氏 (理化学研究所脳科学総合研究センター) 数学と自然科学・社会科学 I「数理脳科学入門」 集中講義 13時00分 〜 14時30分 (京都大学理学部3号館 (数学教室) 110講演室) 甘利 俊一氏 (理化学研究所脳科学総合研究センター) 数学と自然科学・社会科学 I「数理脳科学入門」
- (火) 2010年11月16日
集中講義 13時00分 〜 14時30分 (京都大学理学部3号館 (数学教室) 110講演室) 甘利 俊一氏 (理化学研究所脳科学総合研究センター) 数学と自然科学・社会科学 I「数理脳科学入門」 13時30分 〜 14時30分 第31回 GCOE tea time (京都大学数理解析研究所402号室) 田中 亮吉 (京都大学数学教室) 結晶格子の幾何とスケール極限 15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 大森 俊明 (東北大・理) 高次元調和写像の存在定理に向けて 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館 (数学教室) 552号室) Noriko Mizoguchi (Tokyo Gakugei University) Transversality of stable and Nehari manifolds for a semilinear heat equation 集中講義 18時15分 〜 19時30分 (京都大学理学部3号館 (数学教室) 110講演室) 伊藤 哲史 (京都大学理学研究科数学教室 ) 数学吉田塾・連続講義「楕円曲線の有理点」
- (水) 2010年11月17日
10時00分 〜 11時00分 整数論講演 (京都大学理学部3号館 (数学教室) 108号室) Laurent Fargues ( パリ南大学) Curves and vector bundles in p-adic Hodge theory 11時15分 〜 12時15分 結合系セミナー (京都大学理学部3号館 (数学教室) 108号室) Bryden Cais (ウィスコンシン大学マディソン校) On the restriction of crystalline Galois representations 集中講義 13時00分 〜 14時30分 (京都大学理学部3号館 (数学教室) 110講演室) 甘利 俊一氏 (理化学研究所脳科学総合研究センター) 数学と自然科学・社会科学 I「数理脳科学入門」 15時00分 〜 16時00分 大談話会 (京都大学理学部3号館 (数学教室) 110講演室) 向井 茂 (京大・数理研) ヒルベルトの第14問題と不変式環に対するフェアリンデ型公式 16時50分 〜 17時50分 大談話会 (京都大学理学部3号館 (数学教室) 110講演室) 深谷 賢治 (京大・理) ラグランジュ部分多様体のフレアーホモロジーの計算と応用
- (金) 2010年11月19日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 並河 良典 (京大・理) Slodowy slices and universal Poisson deformations 14時00分 〜 15時00分 NLPDEセミナー (京都大学理学部3号館251号室) Yong Zhou (Zhejiang Normal University) On the Camassa-Holm equation 14時00分 〜 17時00分 京都力学系セミナー (京都大学理学部6号館609号室) 篠原 克寿氏 (Universite de Bourgogne) wild diffeomorphism の新しい例の紹介 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館251号室 ) Satoshi Masaki ( Gakushuin University) 負の指数をもつHartree方程式の解析
- (月) 2010年11月22日
集中講義 15時00分 〜 17時00分 (京都大学理学部3号館 (数学教室) 108号室) 正宗 淳氏 (Penn State Altoona) 数学と自然科学・社会科学 II 「米国における応用数学教育について」
- (水) 2010年11月24日
集中講義 10時00分 〜 12時00分 (京都大学理学部3号館 (数学教室) 108号室) 正宗 淳氏 (Penn State Altoona) 数学と自然科学・社会科学 II 「米国における応用数学教育について」
- (木) 2010年11月25日
集中講義 15時00分 〜 17時00分 (京都大学理学部3号館 (数学教室) 108号室) 正宗 淳氏 (Penn State Altoona) 数学と自然科学・社会科学 II 「米国における応用数学教育について」
- (金) 2010年11月26日
集中講義 10時00分 〜 12時00分 (京都大学理学部3号館 (数学教室) 108号室) 正宗 淳氏 (Penn State Altoona) 数学と自然科学・社会科学 II 「米国における応用数学教育について」 13時00分 〜 15時00分 整数論特別講演 (京都大学理学部3号館 (数学教室) 108号室) Eric Urban (Columbia University) 
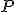-adic Euler systems and 
-adic modular forms
15時00分 〜 16時00分 NLPDEセミナー (京都大学理学部3号館251号室 ) Yong Zhou ( Zhejiang Normal University) Some qualitative studies on the 3D incompressible Navier-Stokes equations 15時30分 〜 17時00分 関西確率論セミナー (京都大学理学部3号館 (数学教室) 552号室) 藤田 岳彦 (一橋大学大学院商学研究科) Special values of the Riemann zeta function via probability theory 16時30分 〜 18時30分 NLPDEセミナー (京都大学理学部3号館251号室) Hideo Takaoka ( Hokkaido University) Well-posedness of the derivative nonlinear Sch\"{o}dinger equation on the one dimensional torus below $H^{1/2}$.
- (月) 2010年11月29日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部3号館 (数学教室) 108号室) Yi-Jun Yao (復旦大学) Hopf cyclic cohomology, Hodge theory, Proper actions (joint with Xiang Tang and Weiping Zhang)
- (火) 2010年11月30日
集中講義 10時30分 〜 12時00分 (京都大学理学部3号館 (数学教室) 127大会議室) Laurent Devineau (Milliman, Inc.) Stochastic Modeling「確率論的モデリング」-- 経済シナリオ（リスク中立とリアルワールド） 集中講義 14時00分 〜 15時30分 (京都大学理学部3号館 (数学教室) 127大会議室) Laurent Devineau (Milliman, Inc.) Stochastic Modeling「確率論的モデリング」-- 死亡・長寿リスクと契約者行動 15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 三石 史人 (筑波大・数理) 崩壊する３次元アレクサンドロフ空間 集中講義 18時15分 〜 19時30分 (京都大学理学部3号館 (数学教室) 110講演室) 伊藤 哲史 (京都大学理学研究科数学教室 ) 数学吉田塾・連続講義「楕円曲線の有理点」
- (水) 2010年12月01日
集中講義 10時30分 〜 12時00分 (京都大学理学部3号館 (数学教室) 127大会議室) Laurent Devineau (Milliman, Inc.) Stochastic Modeling「確率論的モデリング」-- 損害保険リスクのモデリング 13時00分 〜 14時00分 整数論講演 (京都大学理学部3号館 (数学教室) 108号室) James Borger (オーストラリア国立大学) Witt vectors, Lambda-rings, and absolute algebraic geometry 13時00分 〜 14時00分 整数論講演 (京都大学理学部3号館 (数学教室) 108号室) James Borger (オーストラリア国立大学) Witt vectors, Lambda-rings, and absolute algebraic geometry 13時00分 〜 14時00分 整数論講演 (京都大学理学部3号館 (数学教室) 108号室) James Borger (オーストラリア国立大学) Witt vectors, Lambda-rings, and absolute algebraic geometry 16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) 石井 卓 (成蹊大・理工) リー群上の球関数とアルキメデスゼータ積分
- (木) 2010年12月02日
集中講義 10時30分 〜 12時00分 (京都大学理学部3号館 (数学教室) 127大会議室) Laurent Devineau (Milliman, Inc.) Stochastic Modeling「確率論的モデリング」-- エコノミック・キャピタルとソルベンシー��
- (金) 2010年12月03日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) 植田 一石 (大阪大学) Semiorthogonal decompositions in homological mirror symmetry
- (火) 2010年12月07日
13時30分 〜 14時30分 第32回 GCOE tea time (京都大学数理解析研究所402号室) 梶野 直孝 (京都大学情報学研究科) 自己相似フラクタル上のLaplacian・熱方程式 15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 鍛冶 静雄 (山口大・理工) コクセター群の同変シューベルトカリキュラス
- (水) 2010年12月08日
16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 127大会議室) 長田 博文 (九州大学・数理) 平面内の2Dクーロン無限粒子系の確率幾何と力学
- (金) 2010年12月10日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Daniel Allcock (Texas/Kyoto) Completions and Branched Covers
- (火) 2010年12月14日
15時00分 〜 16時00分 第33回 GCOE tea time (京都大学数理解析研究所402号室) 西郷 甲矢人 (京都大学数理解析研究所) 数え上げ論から量子確率論へ 集中講義 18時15分 〜 19時30分 (京都大学理学部3号館 (数学教室) 110講演室) 稲生 啓行 (京都大学理学研究科数学教室 ) 数学吉田塾・連続講義「複素力学系入門」
- (水) 2010年12月15日
15時00分 〜 16時00分 談話会 (京都大学理学部3号館 (数学教室) 110講演室) 阿部 健 (熊本大学・自然科学研究科) 一般テータ関数の空間のstrange duality現象について 16時30分 〜 17時30分 談話会 (京都大学理学部3号館 (数学教室) 110講演室) 岩瀬 則夫 (九州大学・数理) 位相的複雑さとＬＳカテゴリ
- (金) 2010年12月17日
10時30分 〜 12時00分 代数幾何学セミナー (京都大学理学部3号館 (数学教室) 152号室) Joseph H. Silverman (Brown) Amicable Pairs and Aliquot Cycles for Elliptic Curves 13時00分 〜 14時30分 数論合同セミナー (京都大学理学部3号館 (数学教室) 152号室) 山名 俊介 (大阪市大) 非斉次二次形式の局所密度 14時00分 〜 17時00分 京都力学系セミナー (京都大学理学部6号館609号室) 立木 秀樹 (京大・人間環境) テント写像の２次元への拡張と単峰写像について 15時30分 〜 17時30分 NLPDEセミナー (京都大学理学部3号館251号室) Claudio Cacciapuoti ( ) Nonlinear Schroedinger Equation on Star Graphs: Scattering of Fast Solitons 15時30分 〜 17時00分 関西確率論セミナー (京都大学理学部3号館 (数学教室) 552号室) 福島 正俊 (関西大学) 多重連結領域の等角写像と、かがりブラウン運動
- (火) 2010年12月21日
15時00分 〜 16時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) 太田 慎一 (京大・理) アレクサンドロフ空間の熱流について 15時00分 〜 16時00分 第34回 GCOE tea time (京都大学数理解析研究所402号室) 大橋 久範 (名古屋) K3曲面の群作用と有限単純群のつながりについて 17時00分 〜 18時30分 微分トポロジーセミナー (京都大学理学部6号館609号室) Ryszard Nest (University of Compenhagen / RIMS) Homological aspects of Baum-Connes conjecture 集中講義 18時15分 〜 19時30分 (京都大学理学部3号館 (数学教室) 110講演室) 稲生 啓行 (京都大学理学研究科数学教室 ) 数学吉田塾・連続講義「複素力学系入門」
- (水) 2010年12月22日
16時30分 〜 17時30分 談話会 (京都大学数理解析研究所110号室) 梅原 雅顕 (大阪大学・大学院理学研究科) ボンネの定理と曲面上の特異点
［
このページの先頭へ
］